Сила в простоте

Поговорим немного о приватности? Как часто тебе нужно передать какую-то важную цифровую информацию так, что бы быть уверенным, что никто ее не прочитает? В связи с наличием таких программ, как Эшелон и PRISM, это становится особенно актуально.

Современный мир настойчиво диктует нам, что чем сложнее алгоритм, тем он лучше, но это не всегда так. Сегодня я попробую это доказать. Поможет мне в этом относительно малоизвестный криптографический алгоритм, применяемый на практике в основном шпионами и правительствами для передачи секретных данных.

Теория

Итак, немного теории:

Открытый текст -- исходное сообщение, которое нужно зашифровать.
Ключ -- секретная информация, используемая для перевода открытого текста в шифротекст и зачастую обратно.
Шифротекст -- зашифрованное сообщение, которое можно без опаски передавать по открытым каналам связи.

Говорить мы будем об одном из самых простых, но, в то же время, и об одном из самых стойких алгоритмов -- шифре Вернама:

"Шифр Вернама (другое название: англ. One-time pad — схема одноразовых блокнотов) — в криптографии система симметричного шифрования, изобретённая в 1917 году сотрудниками AT&T Мейджором Джозефом Моборном и Гилбертом Вернамом. Шифр Вернама является системой шифрования, для которой доказана абсолютная криптографическая стойкость.
Для произведения шифротекста открытый текст объединяется операцией «исключающее ИЛИ» с ключом (называемым одноразовым блокнотом или шифроблокнотом). При этом ключ должен обладать тремя критически важными свойствами:

• быть истинно случайным;
• совпадать по размеру с заданным открытым текстом;
• применяться только один раз."

Википедия

Для читателя, наверно, не секрет, что все, хранимое и обрабатываемое компьютером можно представить в виде чисел (т.к. компьютер, в переводе а английского -- тот, кто считает, предназначен преимущественно для математических расчетов) в двоичной системе счисления:

• 1 как 1₂
• 2 как 10₂
• 3 как 11₂
• 2013 как 11111011101₂
• строку "text" как 01110100011001010111100001110100₂

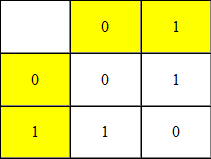
А теперь погорим о т.н. операции «исключающее ИЛИ». Проще всего описать ее с помощью небольшой таблицы, где по горизонтали будут отложены биты сообщения, а по вертикали -- ключа.

Таким образом, при применении Исключающего ИЛИ к открытому тексту 10011101₂ и ключу 10110111₂ получим шифротекст 00101010₂. Что бы расшифровать полученный шифротекст, применим к нему еще раз операцию исключающее ИЛИ и получим 10011101₂, т.е. наш открытый текст.

Как видишь, идеи, заложенные в шифр Вернама, достаточно простые, реализовать их почти на любом современном ЯП можно за пару минут. Однако, возникает вопрос получения абсолютно случайного ключа и его передачи второй стороне. Но если отказаться от абсолютной случайности, все становится предельно просто, особенно в век социальных сетей:

• 1. выбираем случайную фотографию (в целом, нам подойдет абсолютно любой файл, просто сложилось так, что скачать фотографию с соц. сети заметно проще, чем, например, музыку или видео) у себя или друзей (желательно, что бы ее можно было легко отличить от других, но это исключительно для удобства) и используем в качестве ключа;
• 2. при личной встрече сообщаем второй стороне выбранный ключ (описывая или сообщив адрес);
• 3. шифруем с помощью этого ключа и передаем через открытый канал второй стороне секретные данные;
• 4. вторая сторона их расшифровывает;
• 5. при следующей необходимости переходим к первому пункту;

Но не лишен такой подход и слабых сторон: ключевой недостаток шифра Вернама заключается в том, что длина ключа должна быть больше либо равна длине открытого текста, это некритично для небольших txt файлов, но даже маленький, но форматированный документ передать будет не так то уж и просто.

Но есть решение и этой проблемы: использование нескольких ключей взаимно простой длины (т.е. их длины не должны иметь общих делителей, кроме 1, разумеется). Т.е. при использовании двух ключей (длинами 2048 и 2047 байт) у нас два варианта: добавить в конец первого второй ключ (а значит мы сможем зашифровать уже 4095 байт) либо сложить их с помощью все того же исключающего ИЛИ в ключ длинной 4192256 байт (что, согласитесь, неплохо, если эти ключи будут по примерно 25 кб, что примерно равно половине-четвертине обычной фотографии, мы получим ключ длинной в 655334400 байт, что позволит зашифровать документ размером чуть более 600 мб).

Итак, как же можно сложить два ключа с помощью исключающего ИЛИ? Рассмотрим это на примере двух ключей по 3 и 4 бита: 101₂ и 1001₂. Представим их как две "бесконечные"(по сути, закольцованные) ленты и будем постепенно прокручивать их и складывать с помощью исключающего ИЛИ в конечный ключ.

Как видишь, мы с помощью двух ключей динами n=3 и m=4 сгенерировали ключ длинной nm=12 битов. А теперь перейдем к практике.

Практика

Писать я буду на питоне, т.к. это очень простой и выразительный язык, что бы читать программы на нем совсем не обязательно его знать.

Итак, сначала нам понадобится т.н. лента:

def string(data):
    n=0
    while True:
        yield data[n]
        n+=1
        n%=len(data)

Ее задача предельно проста: при каждом запросе возвращать следующий элемент последовательности data, как только последовательность заканчивается -- происходит переход в начало и так до бесконечности.

Что ж, теперь нам нужно превратить произвольный файл в две (можно и больше, но неизвестно, как это отразится на надежности) ленты и получить новую ленту нужной длины.

def genKey(data,l):
    s1, s2= None, None
    if len(data)%2==0:
        data.pop(0) #выбрасываем первый символ, нам нужна нечетная длина
        #обычно это часть сигнатуры типа, одинаковой для всех файлов,
        #так что она нам только мешает
    m=int(len(data)/2) #середина нашего списка
    t1=(data[:m]) #в первую ленту пойдет все до нее 
    t2=(data[m:]) #а во второю -- все остальное
 
    if len(t1)*len(t2)<l:
        raise Exception("Too small data to generate key")
 
    s1=string(t1) #создаем наши ленты
    s2=string(t2) #
 
    out=[] #пустой список
    for i in range(l): #цикл от 0 до l-1
        out+=[next(s1)^next(s2)] #формируем массив, ^ обозначает исключающее ИЛИ
 
    return out

Что бы убедиться в правильности запустим функцию таким образом:

genKey([1,0,1,1,0,0,1],12) => [0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0]

После знака => находится ее вывод, который совпадает с значениями в моей последней таблице, просчитанной вручную. Значит функция работает правильно. Попробуем запросить ключ больше, чем это возможно:

>>> genKey([1,0,1,1,0,0,1],13)
Traceback (most recent call last):
  File "<pyshell#5>", line 1, in <module>
    genKey([1,0,1,1,0,0,1],13)
  File "[цензура] vernam.py", line 19, in genKey
    raise Exception("Too small data to generate key")
Exception: Too small data to generate key

И получим сообщение об ошибке, работает.

Осталось только научиться шифровать файлы. В этом нам поможет следующая функция:

def crypt(datafile, keyfile):
    data=open(datafile,"rb").read()
    key=open(keyfile,"rb").read()
 
    gamma=None
    try:
        gamma=genKey(key,len(data))
    except:
        print("Ключевой файл слишком короткий для шифрования исходного файла.")
        return
 
    out=[data[i]^gamma[i] for i in range(len(data))]
    with open(datafile,"wb") as f:
        f.write(bytes(out))

С целью ее проверки был успешно зашифрован и расшифрован текст данной статьи (разумеется, копия), ключем выступал исходник нашего шифратора.

В заключение

Как видишь, простой не значит слабый. Шифр Вернама уверенно укоренился в областях, требующих сверхсекретности, так почему бы и нам не воспользоваться опытом шпионов?

Исходники: sources/FanOfGun/powerins

______________________________
FanOfGun
2013

Inception E-Zine